Recall that tdistribution have a cumulative probability of 1. If the probability below -2.24 is 0.08 and the probability above 2.24 is also 0.08, so the probability between can be calculated by subtracting the probability below and above from 1.
Solved 3. Suppose that X, Y, Z are three random variables | Chegg.com
Mar 26, 2023Definition: standard normal random variable. A standard normal random variable is a normally distributed random variable with mean μ = 0 μ = 0 and standard deviation σ = 1 σ = 1. It will always be denoted by the letter Z Z. The density function for a standard normal random variable is shown in Figure 5.2.1 5.2. 1.
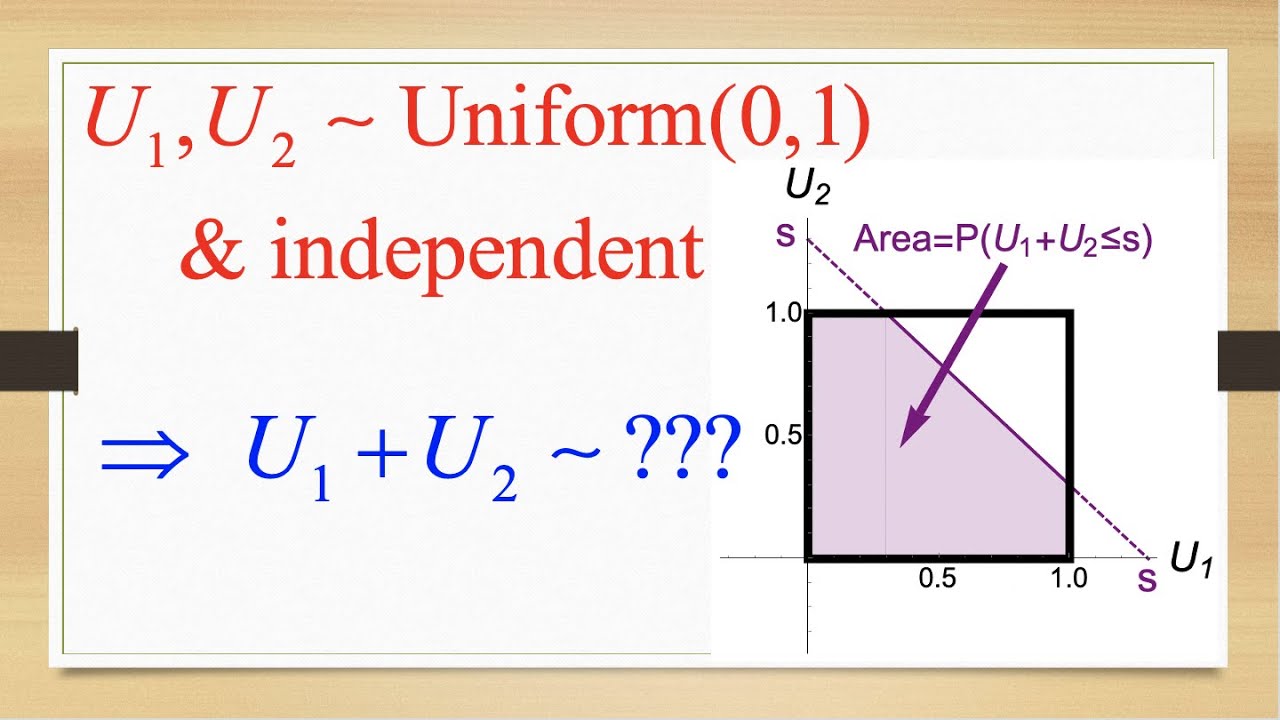
Source Image: m.youtube.com
Download Image
Suppose T and Z are random variables. a. If P (T>2.19)=0.11 and P (T<−2.19)=0.11 , obtain P (−2.19≤T≤2.19). b. If P (−2.05≤Z≤2.05)=0.96 and also P (Z>2.05)=P (Z<−2.05). Find P (Z>2.05). Expert Solution Trending now This is a popular solution! Step by step Solved in 2 steps with 2 images See solution Check out a sample Q&A here Knowledge Booster
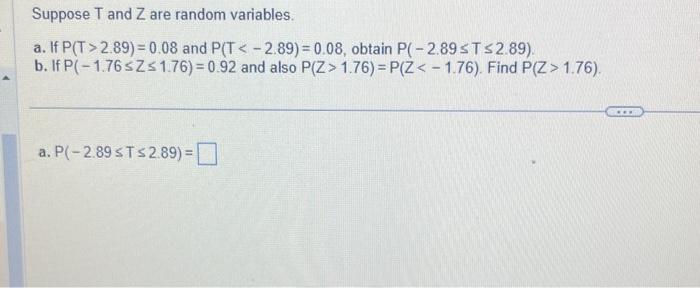
Source Image: chegg.com
Download Image
Solved Suppose T and Z are random variables. a. If | Chegg.com Apr 23, 2022Suppose that X and Y are random variables on a probability space, taking values in R ⊆ R and S ⊆ R, respectively, so that (X, Y) takes values in a subset of R × S. Our goal is to find the distribution of Z = X + Y. Note that Z takes values in T = z ∈ R: z = x + y for some x ∈ R, y ∈ S.

Source Image: medium.com
Download Image
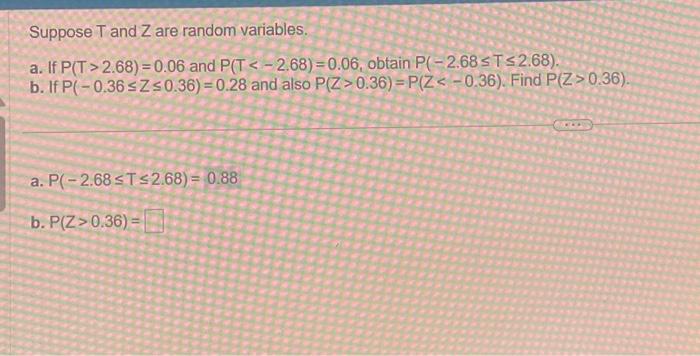
Suppose T And Z Are Random Variables.
Apr 23, 2022Suppose that X and Y are random variables on a probability space, taking values in R ⊆ R and S ⊆ R, respectively, so that (X, Y) takes values in a subset of R × S. Our goal is to find the distribution of Z = X + Y. Note that Z takes values in T = z ∈ R: z = x + y for some x ∈ R, y ∈ S. This problem has been solved! You’ll get a detailed solution from a subject matter expert that helps you learn core concepts. See Answer Question: Suppose T and Z are random variables. a. If P (T>2.68)=0.06 and P (T<−2.68)=0.06, obtain P (−2.68≤T≤2.68). b. If P (−0.36≤Z≤0.36)=0.28 and also P (Z>0.36)=P (Z<−0.36). Find P (Z>0.36). a.
Probability Theory: Continuous Probability Distribution | by Ashish Arora | Medium
Definition. If Z ∼ N ( 0, 1) and U ∼ χ 2 ( r) are independent, then the random variable: T = Z U / r follows a t -distribution with r degrees of freedom. We write T ∼ t ( r). The p.d.f. of T is: f ( t) = Γ ( ( r + 1) / 2) π r Γ ( r / 2) ⋅ 1 ( 1 + t 2 / r) ( r + 1) / 2 for − ∞ < t < ∞. Eric Jang: A Beginner’s Guide to Variational Methods: Mean-Field Approximation
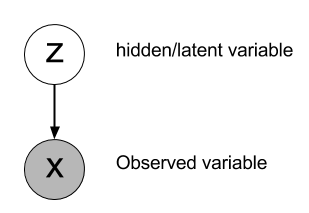
Source Image: blog.evjang.com
Download Image
Continuous Random Variables Definition. If Z ∼ N ( 0, 1) and U ∼ χ 2 ( r) are independent, then the random variable: T = Z U / r follows a t -distribution with r degrees of freedom. We write T ∼ t ( r). The p.d.f. of T is: f ( t) = Γ ( ( r + 1) / 2) π r Γ ( r / 2) ⋅ 1 ( 1 + t 2 / r) ( r + 1) / 2 for − ∞ < t < ∞.
Source Image: saylordotorg.github.io
Download Image
Solved 3. Suppose that X, Y, Z are three random variables | Chegg.com Recall that tdistribution have a cumulative probability of 1. If the probability below -2.24 is 0.08 and the probability above 2.24 is also 0.08, so the probability between can be calculated by subtracting the probability below and above from 1.

Source Image: chegg.com
Download Image
Solved Suppose T and Z are random variables. a. If | Chegg.com Suppose T and Z are random variables. a. If P (T>2.19)=0.11 and P (T<−2.19)=0.11 , obtain P (−2.19≤T≤2.19). b. If P (−2.05≤Z≤2.05)=0.96 and also P (Z>2.05)=P (Z<−2.05). Find P (Z>2.05). Expert Solution Trending now This is a popular solution! Step by step Solved in 2 steps with 2 images See solution Check out a sample Q&A here Knowledge Booster
Source Image: chegg.com
Download Image
Suppose that X, Y, and Z are independent random variables th | Quizlet Expert Solution Trending now This is a popular solution! Step by step Solved in 2 steps with 2 images SEE SOLUTION Check out a sample Q&A here Knowledge Booster Learn more about

Source Image: quizlet.com
Download Image
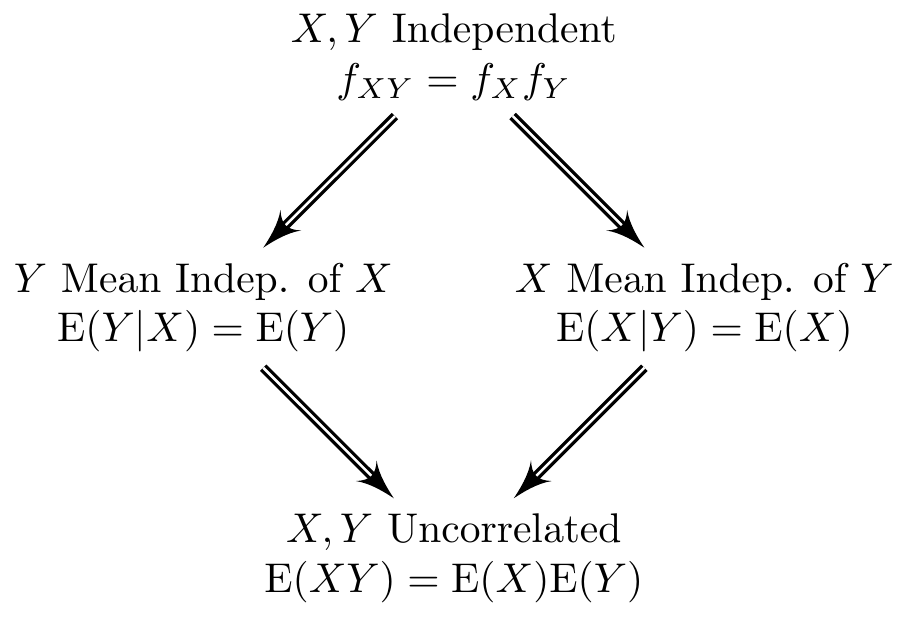
Why Econometrics is Confusing Part II: The Independence Zoo | econometrics. blog Apr 23, 2022Suppose that X and Y are random variables on a probability space, taking values in R ⊆ R and S ⊆ R, respectively, so that (X, Y) takes values in a subset of R × S. Our goal is to find the distribution of Z = X + Y. Note that Z takes values in T = z ∈ R: z = x + y for some x ∈ R, y ∈ S.
Source Image: econometrics.blog
Download Image
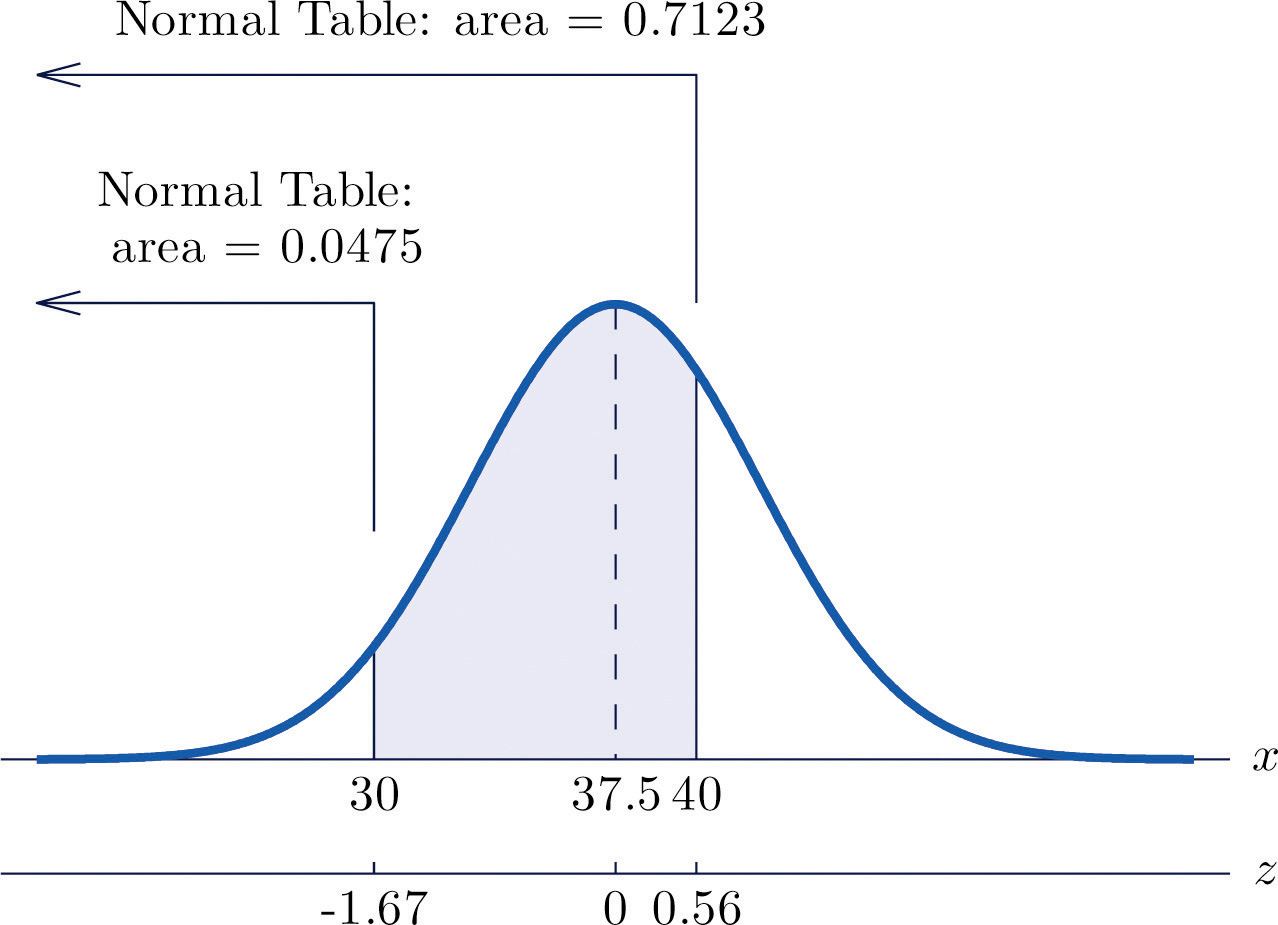
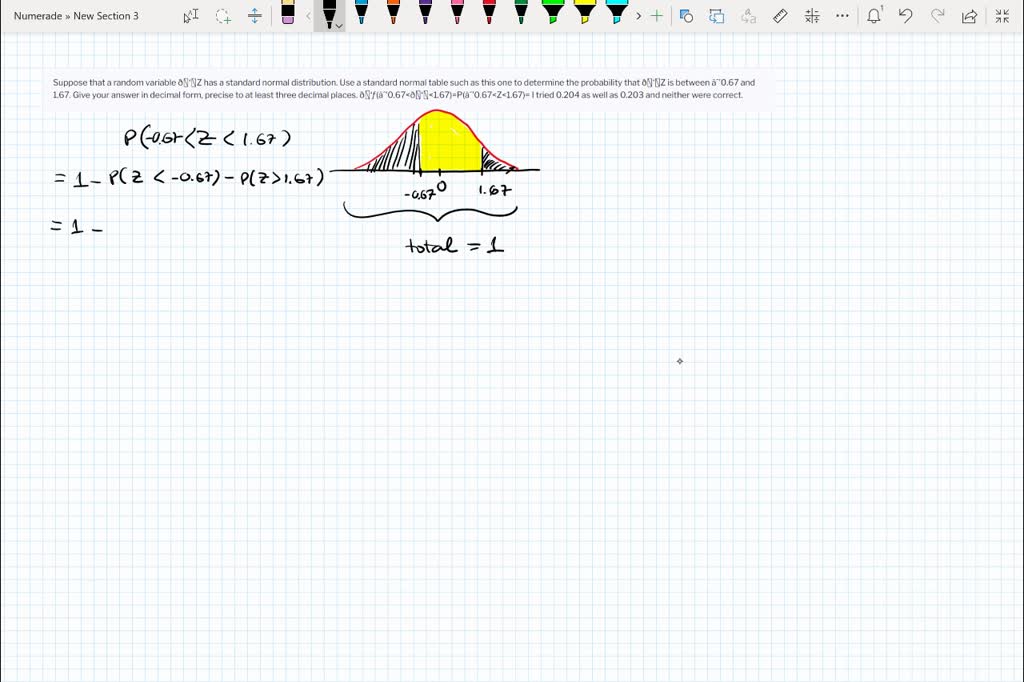
SOLVED: Suppose that a random variable Z has a standard normal distribution. Use a standard normal table such as this one to determine the probability that Z is between -0.67 and 1.67. This problem has been solved! You’ll get a detailed solution from a subject matter expert that helps you learn core concepts. See Answer Question: Suppose T and Z are random variables. a. If P (T>2.68)=0.06 and P (T<−2.68)=0.06, obtain P (−2.68≤T≤2.68). b. If P (−0.36≤Z≤0.36)=0.28 and also P (Z>0.36)=P (Z<−0.36). Find P (Z>0.36). a.
Source Image: numerade.com
Download Image
Continuous Random Variables
SOLVED: Suppose that a random variable Z has a standard normal distribution. Use a standard normal table such as this one to determine the probability that Z is between -0.67 and 1.67. Mar 26, 2023Definition: standard normal random variable. A standard normal random variable is a normally distributed random variable with mean μ = 0 μ = 0 and standard deviation σ = 1 σ = 1. It will always be denoted by the letter Z Z. The density function for a standard normal random variable is shown in Figure 5.2.1 5.2. 1.
Solved Suppose T and Z are random variables. a. If | Chegg.com Why Econometrics is Confusing Part II: The Independence Zoo | econometrics. blog Expert Solution Trending now This is a popular solution! Step by step Solved in 2 steps with 2 images SEE SOLUTION Check out a sample Q&A here Knowledge Booster Learn more about